Up to taking this class, the extent of my competence in Mathematics was the two dimensional plane. Calculus, Geometry, and everything else focused on parabolas, rectangles, circles. But Multivariable Calculus freed me from this pancake of a prison with an infinite number of dimensions. The difference is apparent.
It’s like before I was Integrating this horrible drawing:
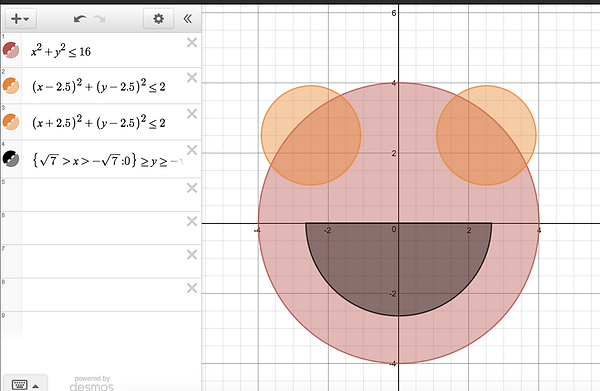
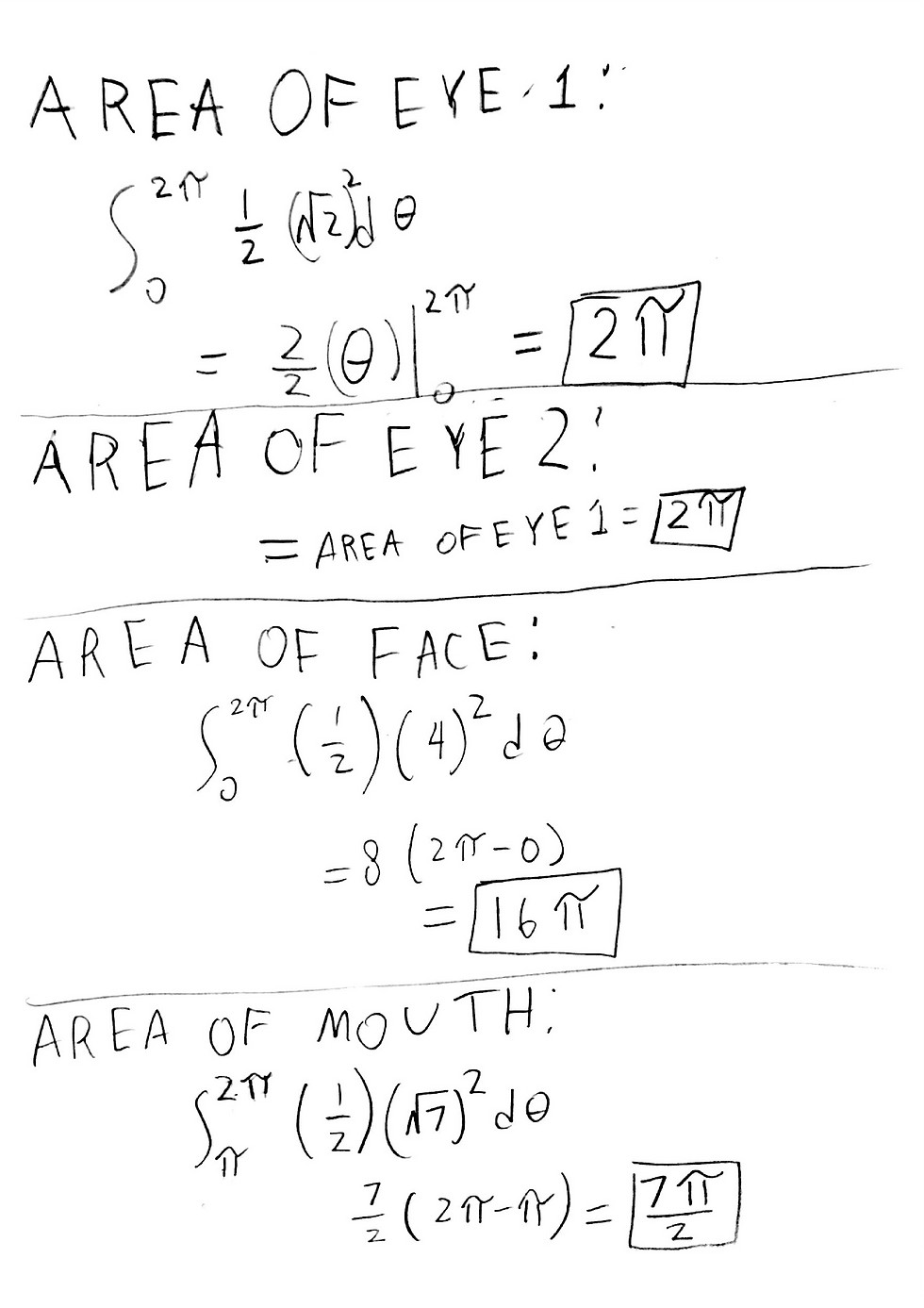
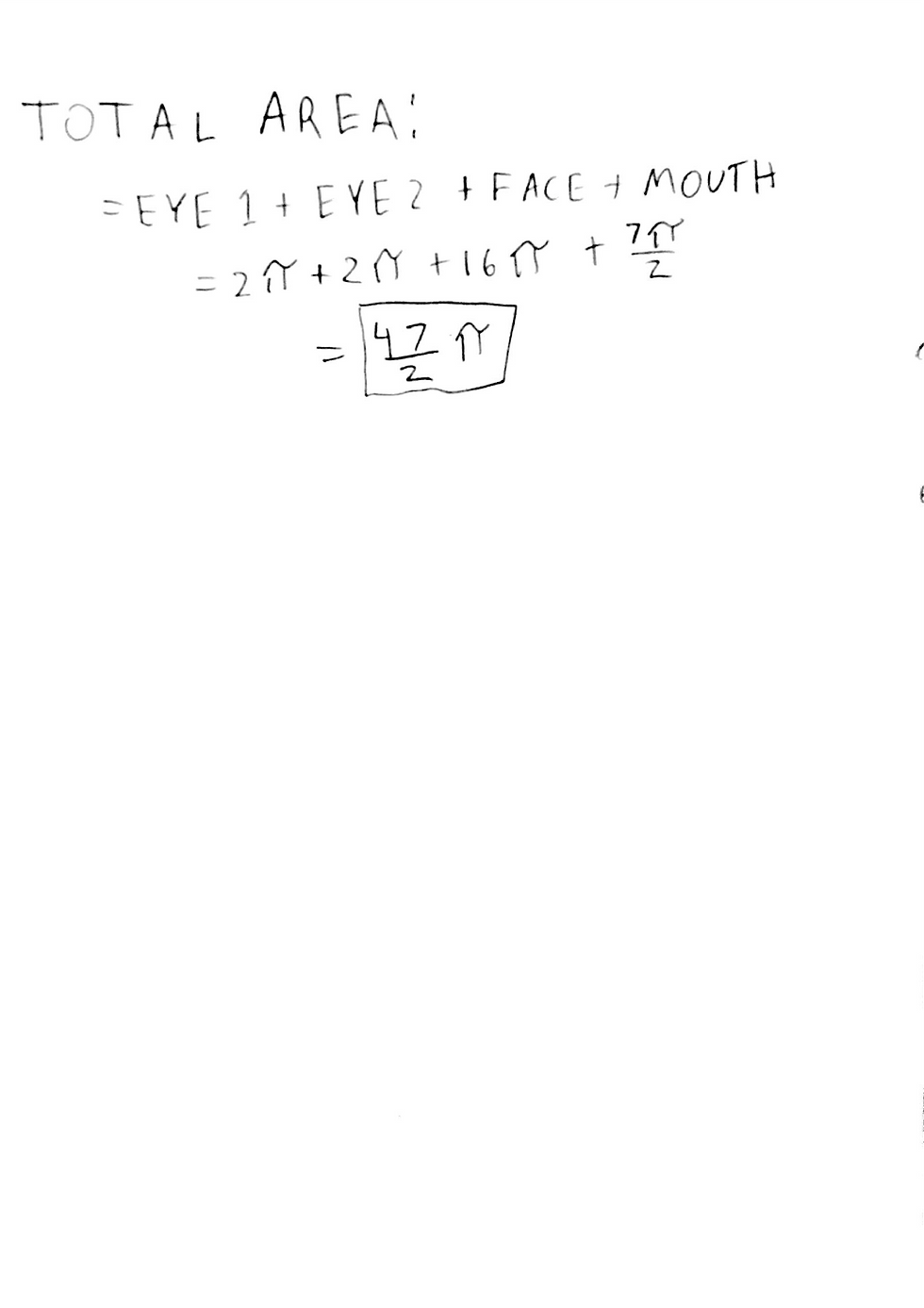

And now I'm integrating horrible drawing:
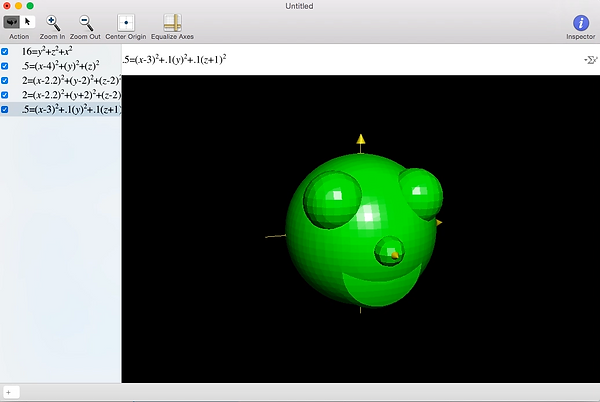
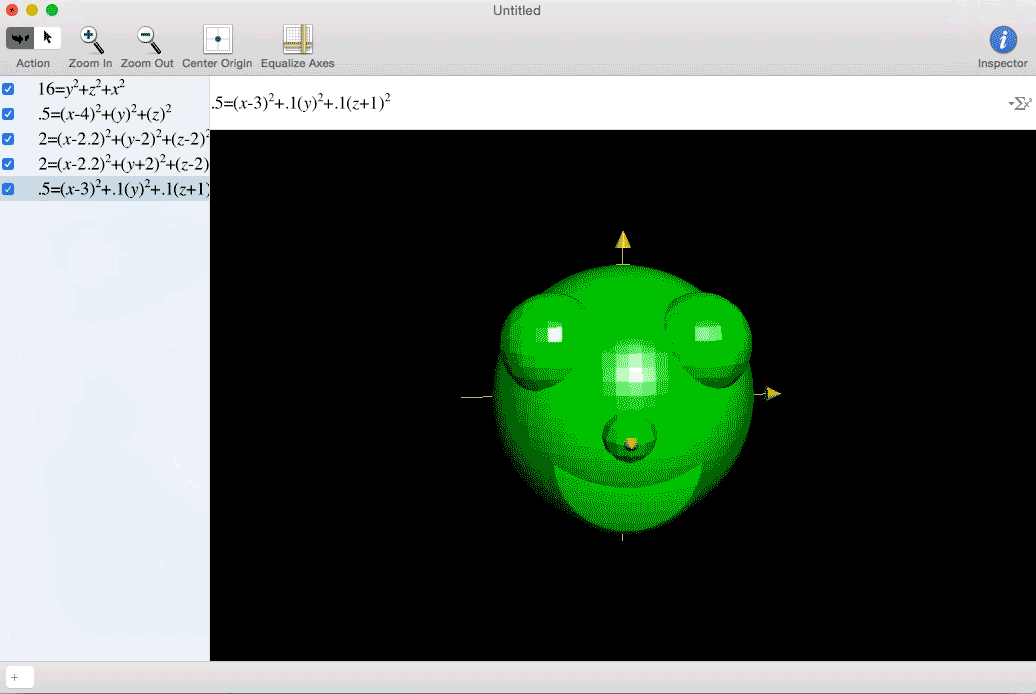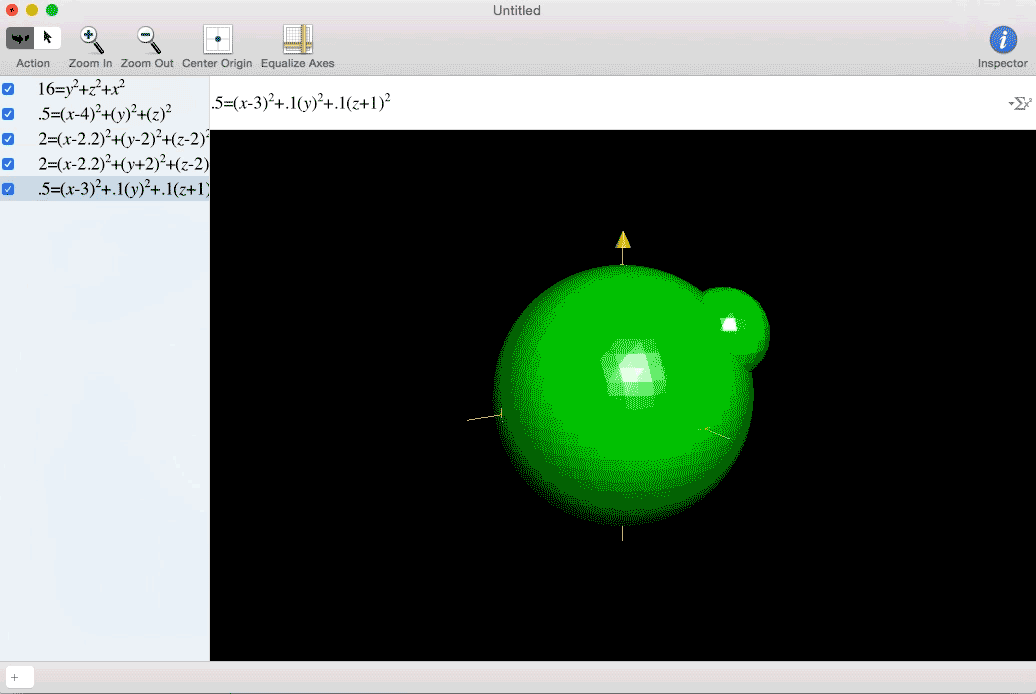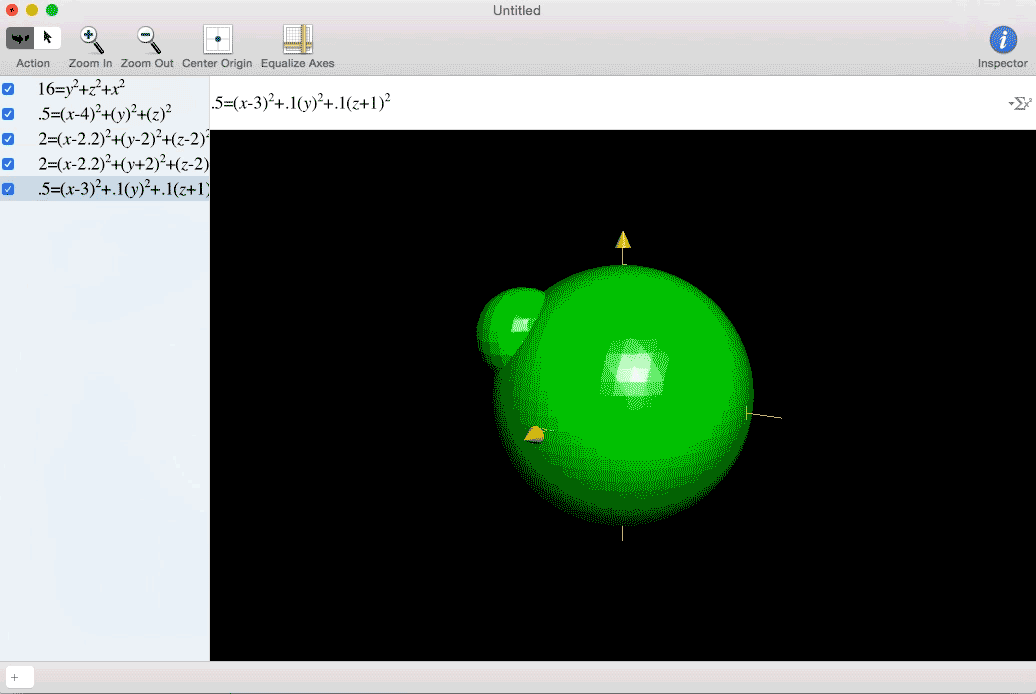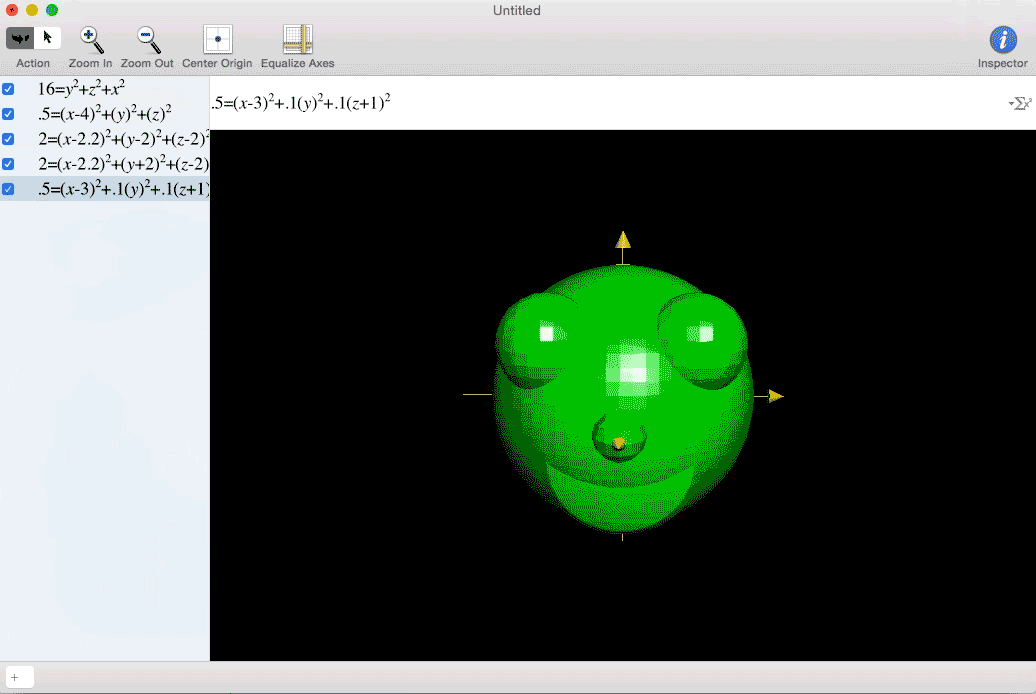


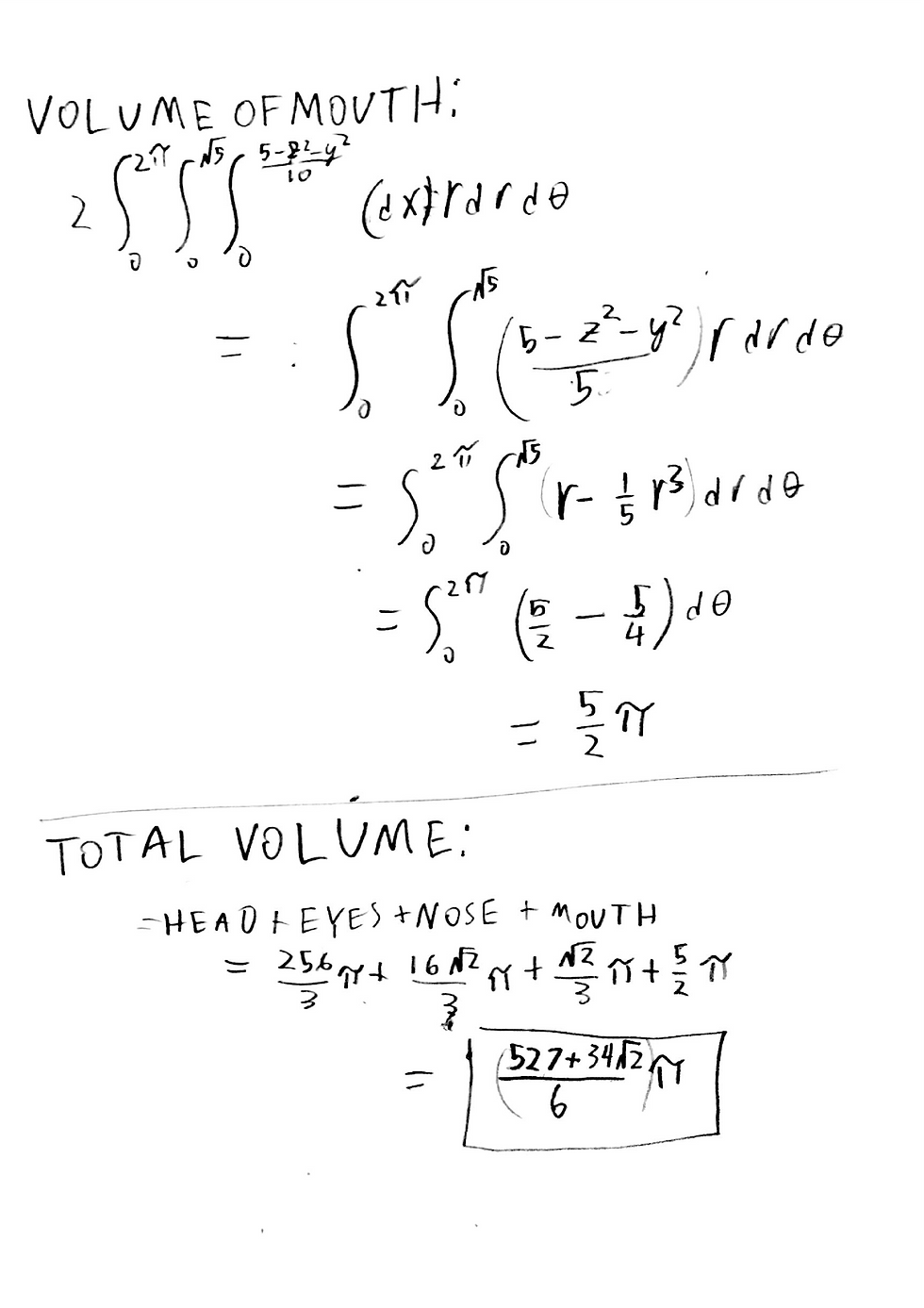

My excitement at my newfound interdimensional freedom must have been comparable to Marty McFly hitting 88 miles per hour.






But there was a darker side to this freedom. The hardest geometry problem in the world just got much more difficult with the extra dimensions.
No longer was I dealing with this sort of thing:
I was faced with this:
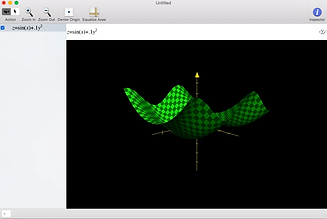


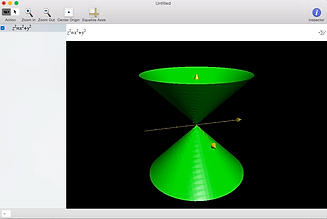
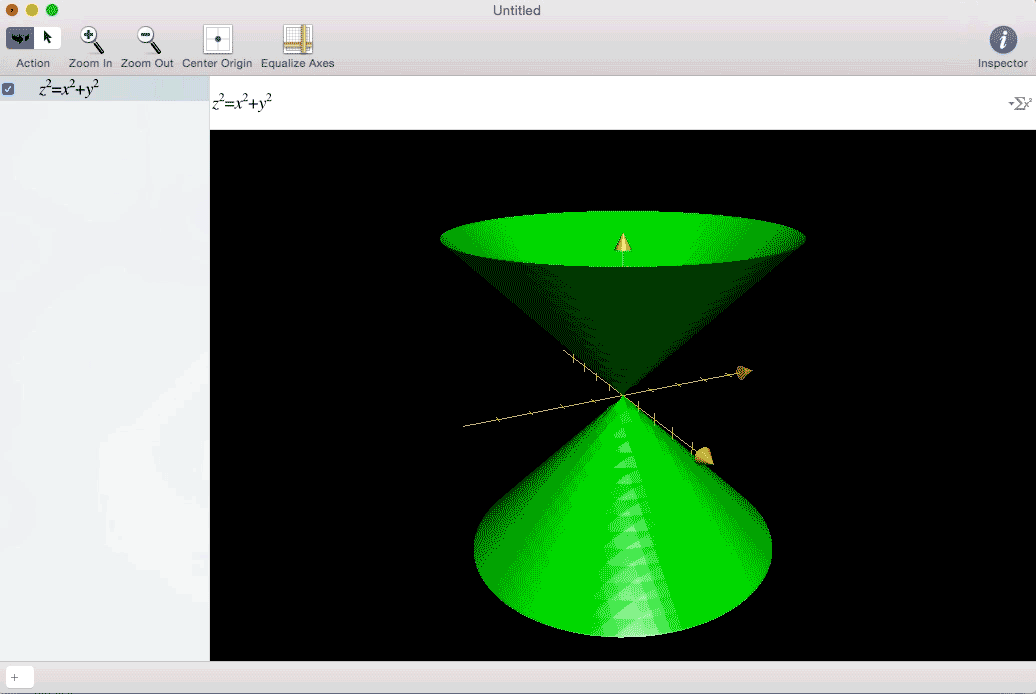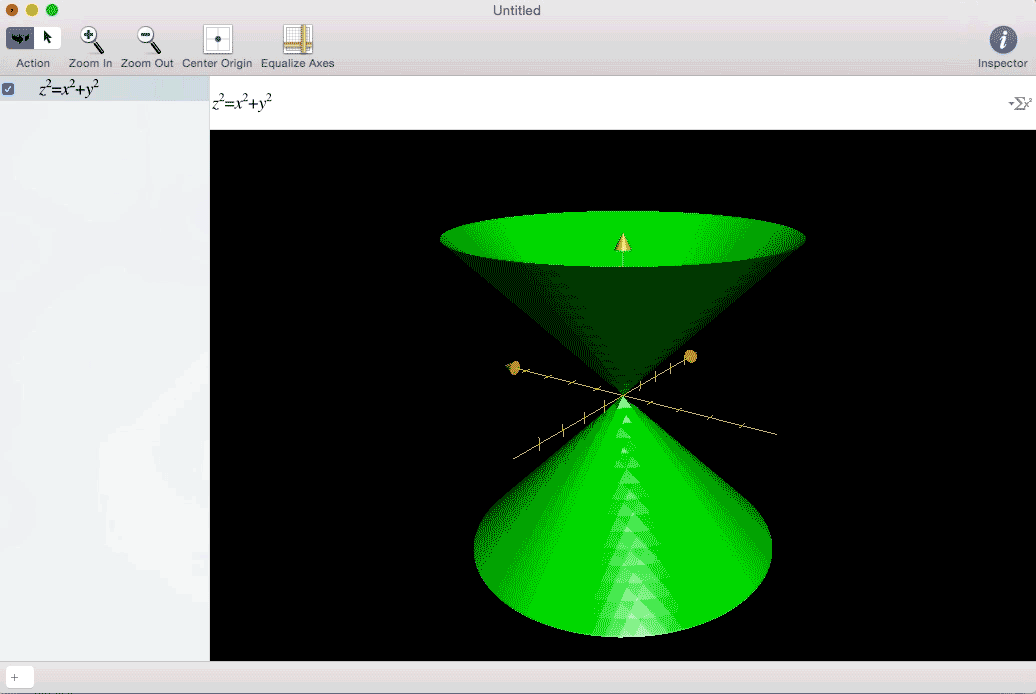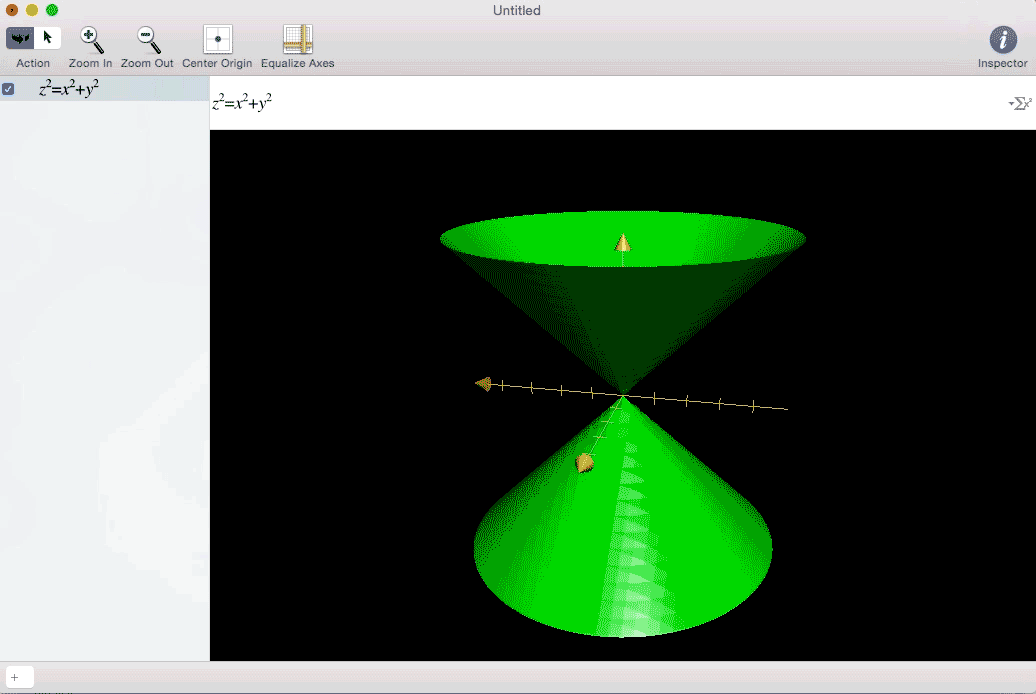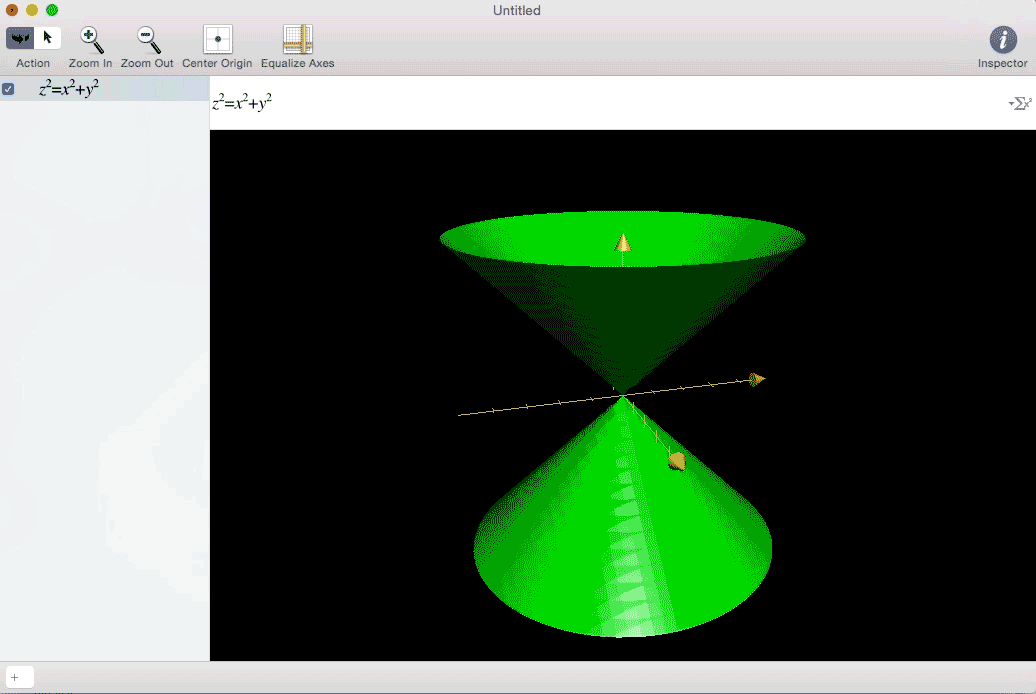

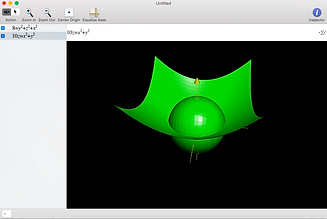



For me, visualizing a problem always helps. I need to understand what it looks like, what its implications are, and why it is what it is. In trying to figure out how to showcase my Multivariable Honors Experience, I wanted to portray mathematics in a visual way. And my favorite visual art form is Cinema. So here go some examples of in movies of what I thought were the three biggest topics in Multivariable Calculus: three-dimensional integration, multidimensional parametric equations, and vector fields
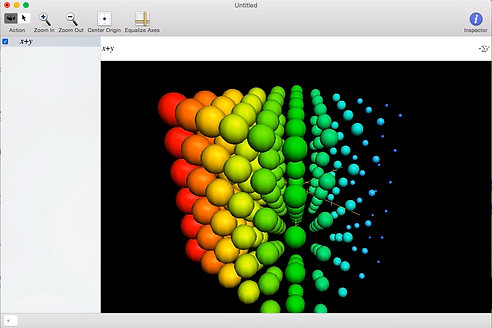
Sometimes you have to integrate a four dimensional concept over a three dimensional space. This is difficult to visualize because we live in a three dimensional world. One way to represent it is to fill a 3D space with different sized spheres to represent larger or smaller values. See the example of w=x+y.


An important application of this integration comes in finding the mass of an object with varying density. Most likely, technicians on the Starkiller base in Star Wars: The Force Awakens had to consider the mass of the star they were consuming so as not to die a horrific death. Because the star was not the same density all the way through, they had to do a bit of multivariable calculus to figure this out.
Because I do not know the actual density of the star from the movie, I based the below calculations off of NASA's statistics on our sun. The total mass comes out to around 1.99*10^30 kg.



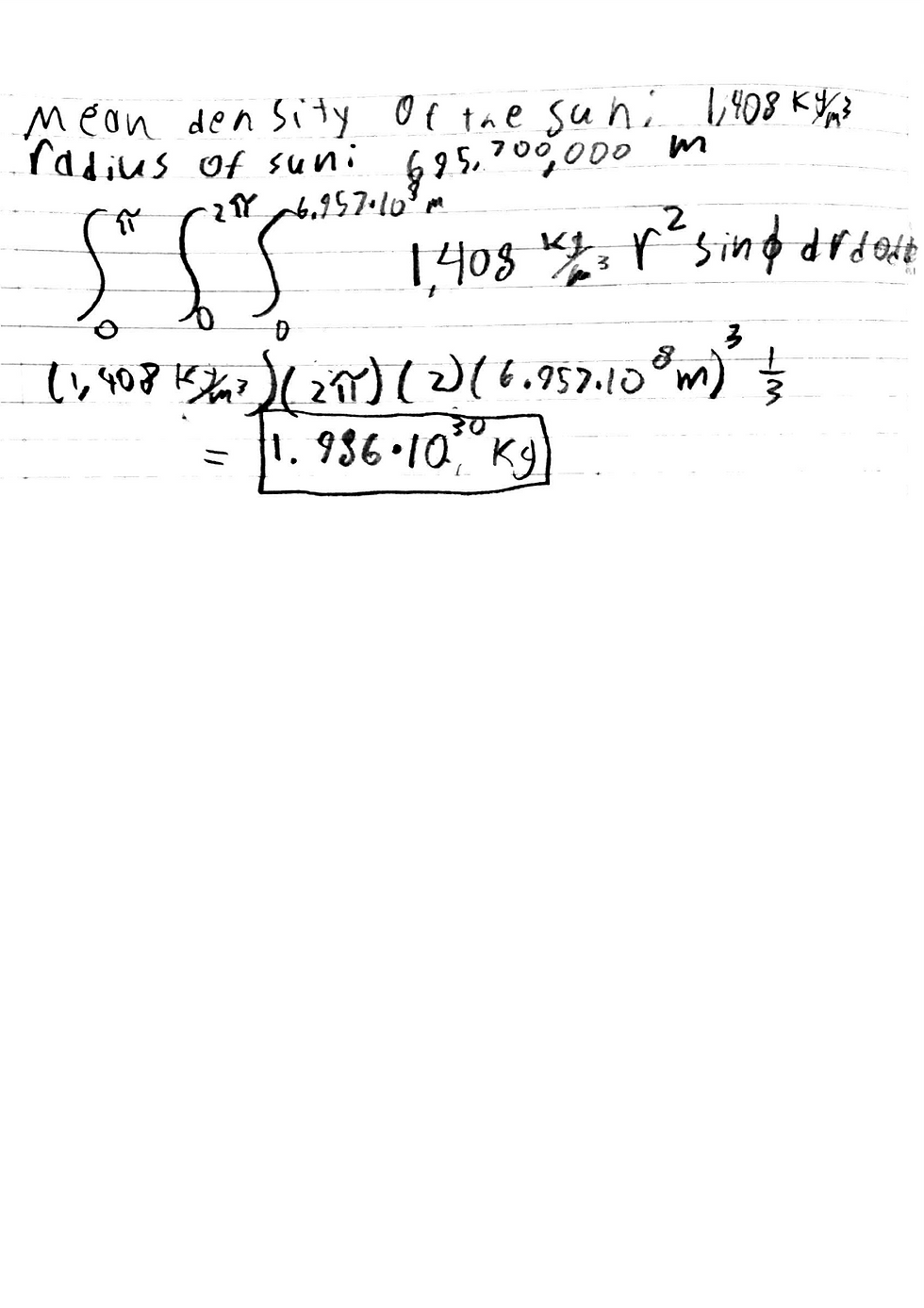
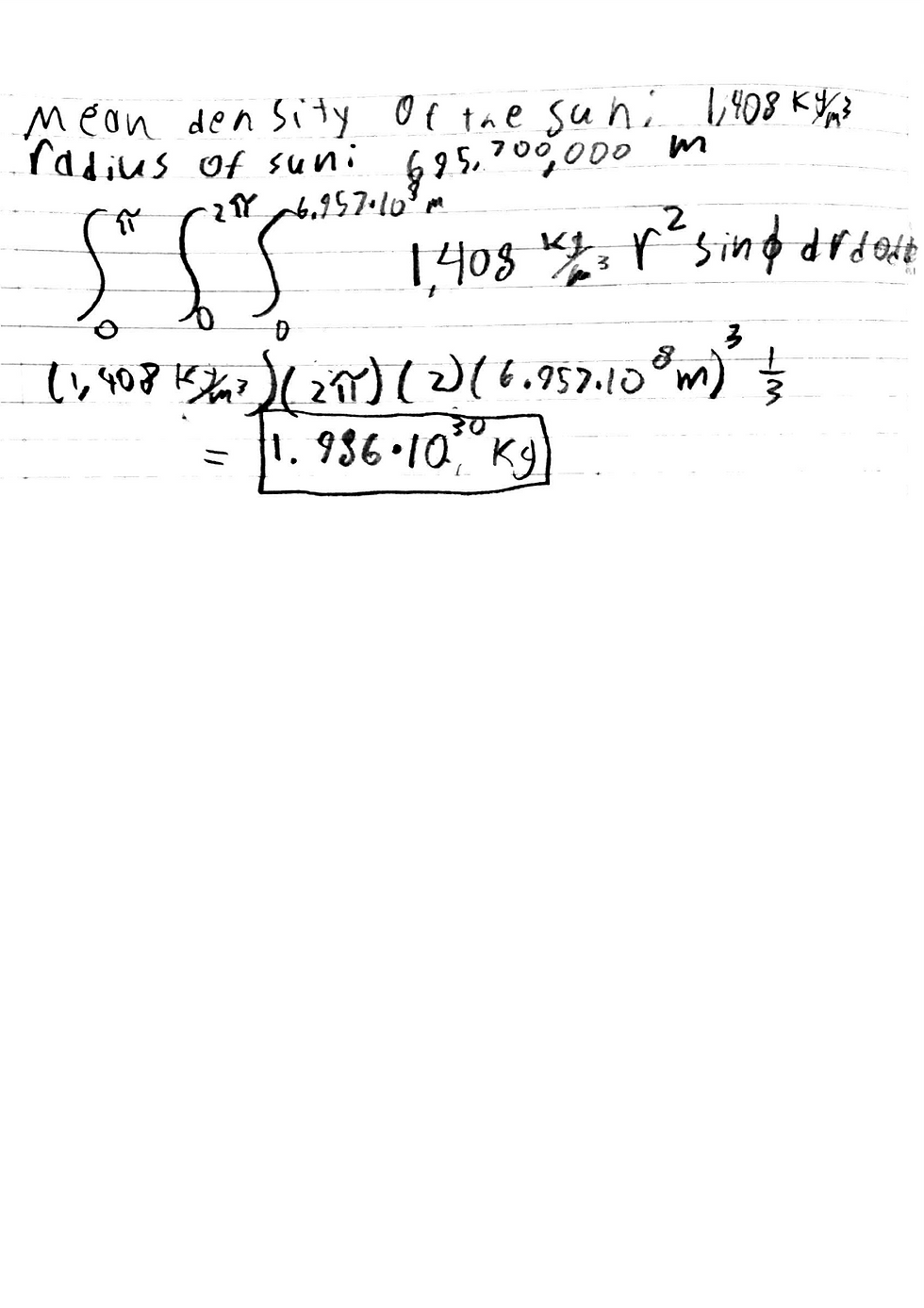
Another prominent topic in Multivariable Calculus is the parametric equation. These are used to show the path that an object takes through two, three, or more dimensions with respect to an independent variable. Usually t, representing time. This lets one create more complicated curves than may be possible with a mere function.
Some of the strangest paths cinematic paths I could think of were from Bill & Ted's Excellent Adventure. On a quest to collect multiple historical figures to pass a history report, they travel through both time and space. For this problem, I came up with a four dimensional parametric equation to represent their final trip from Washington DC 1863 to San Dimas California, 1989 assuming that they did not pass through the earth.



Final parametric equation:
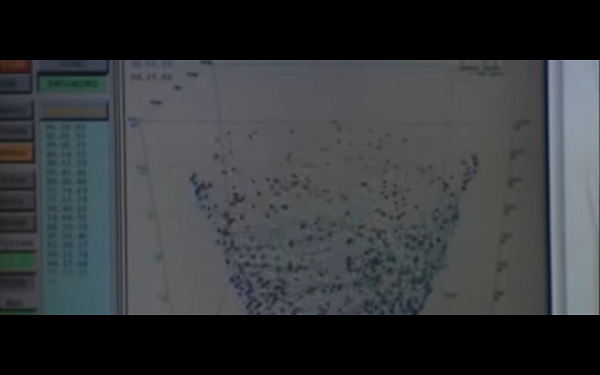
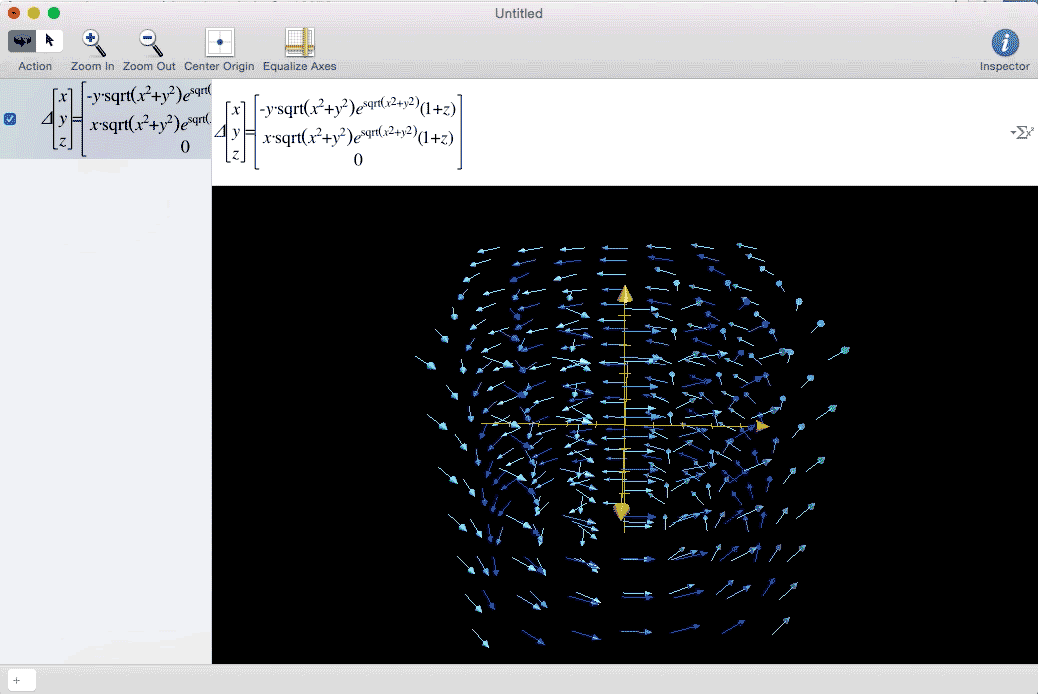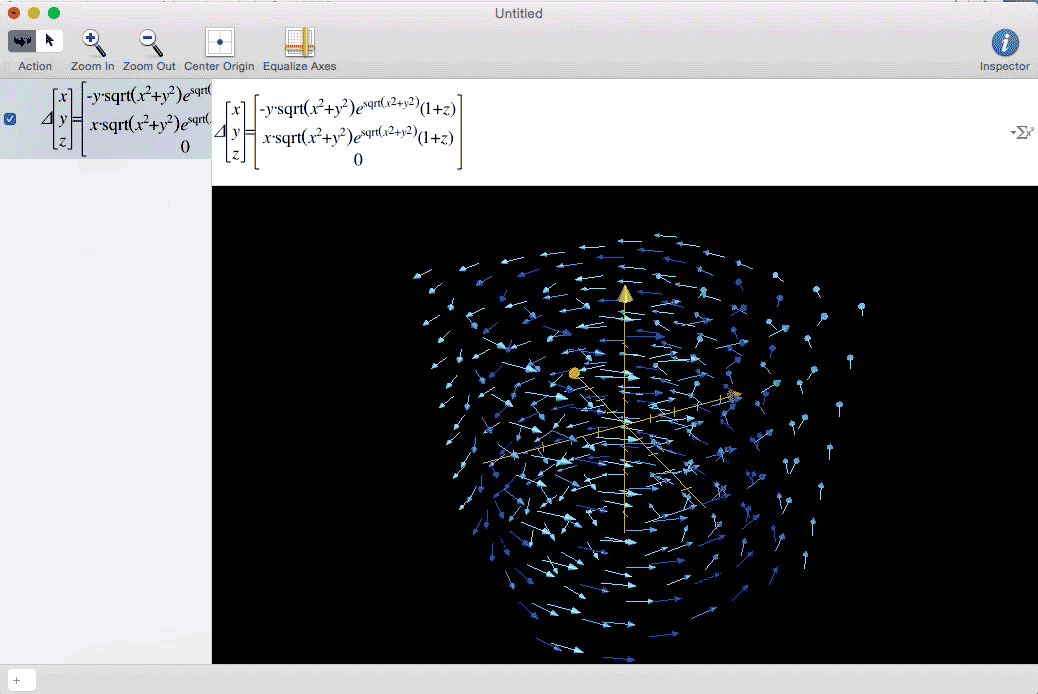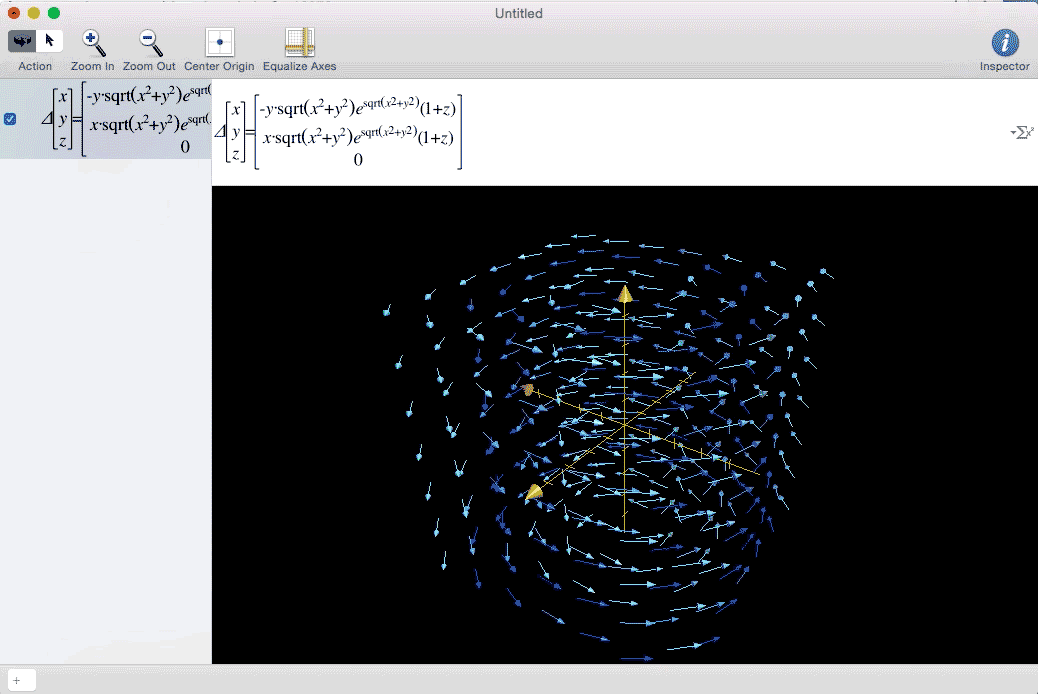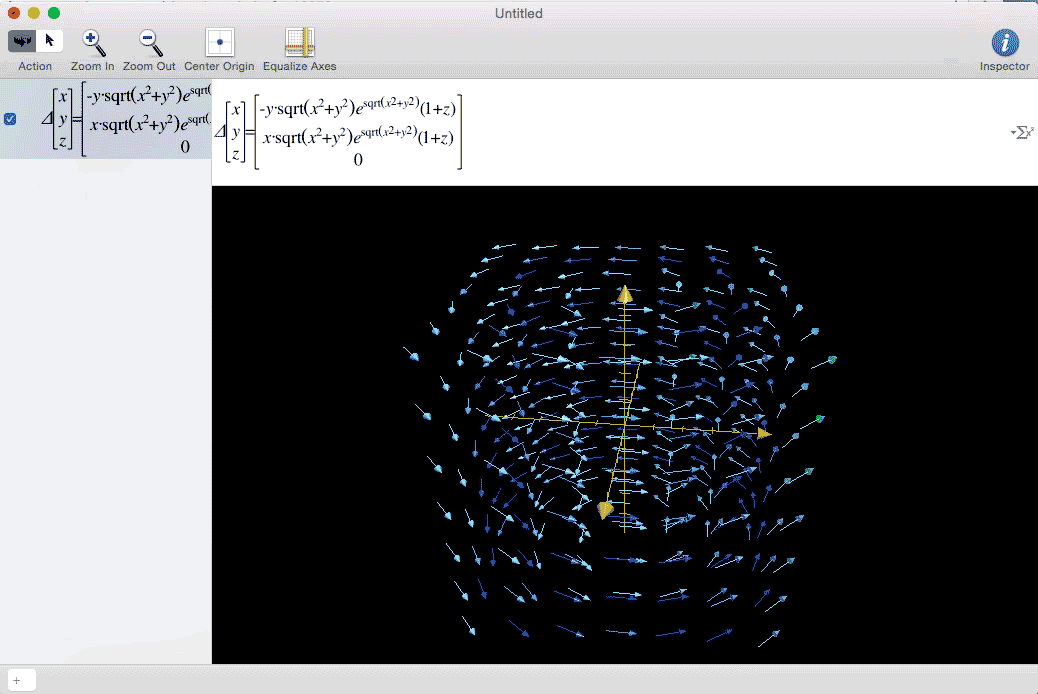
Vector Fields can be used to represent forces that vary in direction and magnitude in 3D spaces. These can be things like gravity, magnetic fields, and wind. A great example of wind analysis takes place in twister. The whole film follows a team of scientists triying to collect data on the inside of a tornado. Below is the data the team finally obtain, which I felt could be represented well as a vector field. Eventually I found an equation that gave the general shape seen in the movie.






Overall, I learned a great deal in Multivariable Calculus. I am intrigued by how my normal understanding of math can be expanded into other dimensions and excited to model it in cool new ways. And already I have been able to apply my knew knowledge to things like physics, circuitry, and to a much more playful extent, cinema.
